The CashValue_SE Model

Overview

The CashValue_SE model projects cashflows of a generic hypothetical savings product. The model is a monthly-step model and projects insurance cashflows of a sample model point at a time. The model can project both new business and in-force policies. The present values of cashflows are also calculated.

By default, the model is configured as follows:

• 4 types of product specs, A, B, C, D are available. The spec parameters are read into product_spec_table from the file product_spec_table.xlsx in the model folder.

• A and B are single premium products with limited policy terms, while C and D are level premium whole life products. A and B are simulate variable annuities, while C and D are simulate variable life.

• By default, 4 model points, 1 for each product type, are set up. The 4 model points are new business policies issued at time 0. The model can also project in-force policies at time 0 or future new business policies issued after time 0.

• Premiums, net of premium loadings if applicable, are transferred to the account value. Maintenance fees and cost-of-insurance charges are deducted from the account value at the beginning of every month. The investment return is then added to/subtracted from the account value. The investment returns are calculated from standard normal random numbers read into std_norm_rand from the file std_norm_rand.csv.

• Upon death, a death benefit is paid. The amount of the death benefit is the greater of the sum assured and the account value. The entire account value is transferred for paying the death benefit.

• Upon lapse, the account value is paid out as surrender benefit. Whether surrender charge applies or not varies by the product types. If it applies, the cash surrender value is the account value net of the surrender charge amount.

• For A and B, the maturity benefit is paid at maturity. The remaining account value is paid as the maturity benefit.

• Depending on the product types, premium loads are collected and the remaining portions of the premiums are transferred to the account value. How much premium loading is collected from each premium varies by the product types, and it is specified in product_spec_table.xlsx. Whether each type has surrender charge and if so its percentages are also specified in the file.

Policy decrement

The number of policies at a certain time can take different values depending on the timing of policy inflows and outflows at the same time. To represent different values for the number of policies depending on the timing of the policy flows, pols_if_at(t, timing) is introduced. pols_if_at(t, timing) calculates the number of policies in-force at time t and has a parameter named timing in addition to t. Strings are passed to timing to indicate at what timing the number of polices in-force is measured.

• "BEF_DECR": Before lapse and death

• "BEF_MAT": Before maturity

• "BEF_NB": Before new business

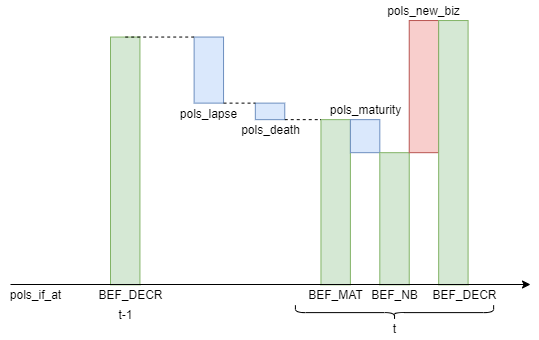
The figure below illustrates how various policy inflows and outflows are modeled in this model for one calculation step from time t-1 to time t.

pols_lapse(t) and pols_death(t) are the number of lapse and death from t-1 to t. It is assumed that policies mature at the beginning of each month, and new business policies enter at the beginning of the month but after the maturity in that month.

Although the default model points are all new business policies, CashValue_SE reads the duration of each model point at time 0 from the model point file. The duration of a model point being N months (N > 0) means N months have elapsed before time 0 since the issue of the model point. If the duration is -N months, the model point is issued N months after time 0.

model_point_table has the duration_mth column, and the column is read into the duration_mth(0). If duration_mth(0) is positive, the model point is in-force policies and the number of policies at time 0 is read from the policy_count column in model_point_table into pols_if_init(), and pols_if_at(0, "BEF_MAT") is set from pols_if_init(). duration_mth() increments by 1 each step. If duration_mth() is negative, policy_count is read into pols_new_biz() when duration_mth() becomes 0.

Account value roll-forward

The account value per policy at each t is calculated from the previous balance by adding cash inflows and subtracting cash outflows. The order and timing of the cashflows are as follows:

• At the beginning of each month, premium net of loadings, if any, is put into the account value.

• At the beginning of the month after the premium inflow, fees are deducted from the account value.

• The investment income is earned on the account value throughout the month. Since policy decrement due to lapse and death is assumed to occur at the middle of the month, half the monthly investment return is assumed to be earned on the account values of the exiting policies.

Basic Usage

Reading the model

Create your copy of the savings library by following the steps on the Quick Start page. The model is saved as the folder named CashValue_SE in the copied folder.

To read the model from Spyder, right-click on the empty space in MxExplorer, and select Read Model. Click the folder icon on the dialog box and select the CashValue_SE folder.

Getting the results

By default, the model has Cells for outputting projection results as listed in the Results section. result_cf() outputs cashflows of the selected model point, result_pv() outputs the present values of the cashflows, result_pols() outputs the decrement table of the model point. All the Cells outputs the results as pandas DataFrame.

See the Quick Start page for how to get the results in an MxConsole and view the results in MxDataViewer.

Changing the model point

The model point to be selected is determined by point_id in Projection. It is 1 by default. model_point_table contains 4 model points as a pandas DataFrame. To change the model point to another one, set the other model point’s ID to point_id. Setting the new point_id clears all the values of Cells that are specific to the previous model point.

Getting multiple results

The Projection space is parameterized with point_id, i.e. the Projection space can have dynamic child spaces, such as Projection[1], Projection[2], Projection[3] …, each of which represents the Projection for each of the model points.

Note

Getting results for too many dynamic child spaces takes a considerable amount of time. The default CashValue_SE model would take more than a minute for 1000 model points on an ordinary spec PC. To calculate for many model points, consider using the CashValue_ME model.

Model Specifications

The CashValue_SE model has only one UserSpace, named Projection, and all the Cells and References are defined in the space.

The Projection Space

The main Space in the CashValue_SE model.

Projection is the only Space defined in the CashValue_SE model, and it contains all the logic and data used in the model.

Parameters and References

(In all the sample code below, the global variable Projection refers to the Projection Space.)

point_id

The ID of the selected model point. point_id is defined as a Reference, and its value is used for determining the selected model point. By default, 1 is assigned. To select another model point, assign its model point ID to it:

>>> Projection.point_id = 2

point_id is also defined as the parameter of the Projection Space, which makes it possible to create dynamic child space for multiple model points:

>>> Projection.parameters
('point_id',)

>>> Projection[1]
<ItemSpace CashValue_SE.Projection[1]>

>>> Projection[2]
<ItemSpace CashValue_SE.Projection[2]>

See also

• model_point_table

• model_point()

model_point_table

All model points as a DataFrame. By default, 4 model points are defined. The DataFrame has an index named point_id, and model_point() returns a record as a Series whose index value matches point_id. The DataFrame has the following columns:

• spec_id

• age_at_entry

• sex

• policy_term

• policy_count

• sum_assured

• duration_mth

• premium_pp

• av_pp_init

Cells defined in Projection with the same names as these columns return the corresponding column’s values for the selected model point.

>>> Projection.model_poit_table
         spec_id  age_at_entry sex  ...  premium_pp  av_pp_init
poind_id                            ...
1              A            20   M  ...      500000           0
2              B            50   M  ...      500000           0
3              C            20   M  ...        1000           0
4              D            50   M  ...        1000           0

[4 rows x 10 columns]

The DataFrame is saved in the Excel file model_point_samples.xlsx placed in the model folder. model_point_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file. The DataFrame has the injected attribute of _mx_dataclident:

>>> Projection.model_point_table._mx_dataclient
<PandasData path='model_point_table_samples.xlsx' filetype='excel'>

See also

• point_id

• model_point()

• age_at_entry()

• sex()

• policy_term()

• pols_if_init()

• sum_assured()

• duration_mth()

• premium_pp()

• av_pp_init()

disc_rate_ann

Annual discount rates by duration as a pandas Series.

>>> Projection.disc_rate_ann
year
0      0.00000
1      0.00555
2      0.00684
3      0.00788
4      0.00866

146    0.03025
147    0.03033
148    0.03041
149    0.03049
150    0.03056
Name: disc_rate_ann, Length: 151, dtype: float64

The Series is saved in the Excel file disc_rate_ann.xlsx placed in the model folder. disc_rate_ann is created by Projection’s new_pandas method, so that the Series is saved in the separate file. The Series has the injected attribute of _mx_dataclident:

>>> Projection.disc_rate_ann._mx_dataclient
<PandasData path='disc_rate_ann.xlsx' filetype='excel'>

See also

• disc_rate_mth()

• disc_factors()

mort_table

Mortality table by age and duration as a DataFrame. See basic_term_sample.xlsx included in this library for how the sample mortality rates are created.

>>> Projection.mort_table
            0         1         2         3         4         5
Age
18   0.000231  0.000254  0.000280  0.000308  0.000338  0.000372
19   0.000235  0.000259  0.000285  0.000313  0.000345  0.000379
20   0.000240  0.000264  0.000290  0.000319  0.000351  0.000386
21   0.000245  0.000269  0.000296  0.000326  0.000359  0.000394
22   0.000250  0.000275  0.000303  0.000333  0.000367  0.000403
..        ...       ...       ...       ...       ...       ...
116  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
117  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
118  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
119  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
120  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000

[103 rows x 6 columns]

The DataFrame is saved in the Excel file mort_table.xlsx placed in the model folder. mort_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file. The DataFrame has the injected attribute of _mx_dataclident:

>>> Projection.mort_table._mx_dataclient
<PandasData path='mort_table.xlsx' filetype='excel'>

See also

• mort_rate()

• mort_rate_mth()

std_norm_rand

Random numbers drawn from the standard normal distribution.

A Series of random numbers drawn from the standard normal distribution indexed with scen_id and t. Used for generating investment returns. See inv_return_table().

scen_id

Selected scenario ID

An integer indicating the selected scenario ID. scen_id is referenced in by inv_return_mth() as one of the keys to select a scenario from std_norm_rand.

surr_charge_table

Surrender charge rates by duration.

A DataFrame of multiple patterns of surrender charge rates by duration. The column labels indicate surr_charge_id(). By default, "type_1", "type_2" and "type_3" are defined.

product_spec_table

Table of product specs.

A DataFrame of product spec parameters by spec_id. model_point_table and product_spec_table columns are joined in model_point_table_ext(), and the product_spec_table columns become part of the model point attributes. The product_spec_table columns are read by the Cells with the same names as the columns:

• premium_type()

• has_surr_charge()

• surr_charge_id()

• load_prem_rate()

• is_wl()

>>> Projection.product_spec_table
        premium_type  has_surr_charge surr_charge_id  load_prem_rate  is_wl
spec_id
A             SINGLE            False            NaN            0.10  False
B             SINGLE             True         type_1            0.00  False
C              LEVEL            False            NaN            0.10   True
D              LEVEL             True         type_3            0.05   True

np

The numpy module.

pd

The pandas module.

Projection parameters

The time step of the model is monthly. Cashflows and other time-dependent variables are indexed with t.

Projection is carried out separately for individual model points. proj_len() calculates the number of months to be projected for the selected model point.

Cashflows and other flows that accumulate throughout a period indexed with t denote the sums of the flows from t til t+1. Balance items indexed with t denote the amount at t.

proj_len()

Projection length in months

Model point data

The model point data stored in an Excel file named model_point_table.xlsx under the model folder is read into model_point_table. Policy attributes that only vary by product spec are stored separately in another Excel file named product_spec_table.xlsx, and read into product_spec_table. The product_spec_table attributes are joined with model_point_table in model_point_table_ext() and referenced from model_point().

model_point()	The selected model point as a Series
model_point_table_ext()	Extended model point table
sex()	The sex of the selected model point
sum_assured()	The sum assured of the selected model point
policy_term()	The policy term of the selected model point.
age(t)	The attained age at time t.
age_at_entry()	The age at entry of the selected model point
duration(t)	Duration of the selected model point at t in years
duration_mth(t)	Duration of the selected model point at t in months
has_surr_charge()	Whether surrender charge applies
is_wl()	Whether the model point is whole life
load_prem_rate()	Rate of premium loading
surr_charge_id()	ID of surrender charge pattern
premium_type()	Type of premium payment
av_pp_init()	Initial account value per policy

Assumptions

The mortality table is stored in an Excel file named mort_table.xlsx under the model folder, and is read into mort_table as a DataFrame. mort_rate() looks up mort_table and picks up the annual mortality rate to be applied for the selected model point at time t. mort_rate_mth() converts mort_rate() to the monthly mortality rate to be applied during the month starting at time t.

The discount rate data is stored in an Excel file named disc_rate_ann.xlsx under the model folder, and is read into disc_rate_ann as a Series.

The lapse by duration is defined by a formula in lapse_rate(). expense_acq() holds the acquisition expense per policy at t=0. expense_maint() holds the maintenance expense per policy per annum. The maintenance expense inflates at a constant rate of inflation given as inflation_rate().

mort_table_last_age()	The last age of mortality tables
mort_rate(t)	Mortality rate to be applied at time t
mort_rate_mth(t)	Monthly mortality rate to be applied at time t
disc_factors()	Discount factors.
disc_rate_mth()	Monthly discount rate
lapse_rate(t)	Lapse rate
expense_acq()	Acquisition expense per policy
expense_maint()	Annual maintenance expense per policy
inflation_factor(t)	The inflation factor at time t
inflation_rate()	Inflation rate

Policy values

By default, the amount of death benefit for each policy (claim_pp()) is set equal to sum_assured.

premium_pp() is the single premium amount if the model point represents single premium policies (i.e. premium_type() is "SINGLE"), or the monthly premium amount if the model point represents level premium policies (i.e. premium_type() is "LEVEL").

claim_pp(t, kind)	Claim per policy
premium_pp(t)	Premium amount per policy
maint_fee_rate()	Maintenance fee per account value
coi_rate(t)	Cost of insurance rate per account value
surr_charge_rate(t)	Surrender charge rate

Policy decrement

At t=0

If the selected model point represents in-force policies, i.e. the duration_mth of the model point in model_point_table is positive, pols_if_at(0, "BEF_MAT") is set to the value through pols_if_init().

At each projection step

pols_if_at(t, timing) represents the number of policies at t. The timing parameter can take the following string values.

• "BEF_MAT": Before maturity

• "BEF_NB": Before new business

• "BEF_DECR": Before lapse and death

Policy flows and in-force at each timing from t-1 to t are calculated recursively as follows:

• pols_if_at(t-1, "BEF_DECR") is calculated by adding pols_new_biz(t-1) to pols_if_at(t-1, "BEF_NB").

• pols_if_at(t, "BEF_MAT") is calculated by deducting pols_lapse(t) and pols_death(t) from pols_if_at(t-1, "BEF_DECR").

• pols_if_at(t, "BEF_NB") is calculated by deducting pols_maturity(t) from pols_if_at(t, "BEF_MAT").

• pols_if_at(t, "BEF_DECR") is calculated by pols_new_biz(t) from pols_if_at(t, "BEF_NB").

It is assumed that policies mature at the beginning of each month, and new business policies enter at the beginning of the month but after the maturity in that month. pols_if(t) is an alias for pols_if_at(t, "BEF_MAT").

The figure below illustrates how various policy inflows and outflows are modeled in this model for one calculation step from time t-1 to time t.

pols_death(t)	Number of death
pols_if(t)	Number of policies in-force
pols_if_at(t, timing)	Number of policies in-force
pols_if_init()	Initial number of policies in-force
pols_lapse(t)	Number of lapse
pols_maturity(t)	Number of maturing policies
pols_new_biz(t)	Number of new business policies

Account Value

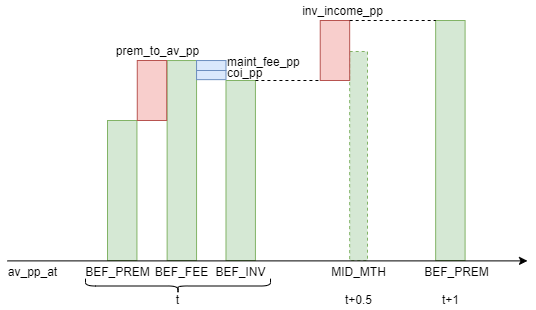
av_pp_at(t, timing) calculates the account value per policy at t. Since av_pp_at() can take multiple values for the same t depending on the timing of various cashflows into and out of the account value, the second parameter timing is used to specify the timing of measuring the account value.

av_pp_at(t, 'BEF_PREM') indicates the account value before premium payment for the month. At time 0, it is read from av_pp_init(), otherwise its calculated from the previous period as av_pp_at(t-1, 'BEF_INV') plus inv_income_(t-1).

av_pp_at(t, 'BEF_FEE') indicates the account value after the premium payment before fee deduction, and is calculated as av_pp_at(t, 'BEF_PREM') plus prem_to_av_pp().

av_pp_at(t, 'BEF_INV') indicates the account value after then fee deduction before earning investment yield, and is calculated as av_pp_at(t, 'BEF_FEE') minus maint_fee_pp() and coi_pp().

av_pp_at(t, 'MID_MTH') indicates the account value at t+0.5, and half of inv_income() is earned. av_pp_at(t, 'MID_MTH') is for policies exiting by lapse and death during the month.

inv_income(t)	Investment income on account value
inv_income_pp(t)	Investment income on account value per policy
inv_return_mth(t)	Rate of investment return
inv_return_table()	Table of investment return rates
av_pp_at(t, timing)	Account value per policy
net_amt_at_risk(t)	Net amount at risk per policy
coi_pp(t)	Cost of insurance charges per policy
prem_to_av_pp(t)	Per-policy premium portion put in the account value
maint_fee_pp(t)	Maintenance fee per policy
av_at(t, timing)	Account value in-force
prem_to_av(t)	Premium portion put in account value
claims_from_av(t, kind)	Account value taken out to pay claim
claims_over_av(t)	Claim in excess of account value
coi(t)	Cost of insurance charges
maint_fee(t)	Maintenance fee deducted from account value
av_change(t)	Change in account value
check_av_roll_fwd()	Check account value roll-forward

Cashflows

Cashflows are calculated as its per-policy amount times the number of policies.

The expense cashflow consists of acquisition expenses at issue and monthly maintenance expenses spent each month.

By default, commissions are defined as 5% premiums.

surr_charge(t)	Surrender charge
claims(t[, kind])	Claims
commissions(t)	Commissions
premiums(t)	Premium income
expenses(t)	Expenses
net_cf(t)	Net cashflow

Margin Analysis

net_cf() can be expressed as the sum of expense and mortality margins. The expense margin is defined as the sum of premium loading, surrender charge and maintenance fees net of commissions and expenses. The mortality margin is defined coi() net of claims_over_av().

margin_expense(t)	Expense margin
margin_mortality(t)	Mortality margin
check_margin()	Check consistency between net cashflow and margins

Present values

The Cells whose names start with pv_ are for calculating the present values of the cashflows indicated by the rest of their names. pv_pols_if() is not used in CashValue_SE and BasicTerm_ME.

pv_claims([kind])	Present value of claims
pv_commissions()	Present value of commissions
pv_expenses()	Present value of expenses
pv_net_cf()	Present value of net cashflows.
pv_pols_if()	Present value of policies in-force
pv_premiums()	Present value of premiums
pv_av_change()	Present value of change in account value
pv_inv_income()	Present value of investment income
check_pv_net_cf()	Check present value summation

Results

result_cf() outputs the cashflows of the selected model point as a DataFrame:

>>> result_cf()
       Premiums        Death  ...  Change in AV  Net Cashflow
0    50000000.0   999.844857  ...  4.447174e+07  2.033342e+06
1           0.0   991.084783  ... -1.065060e+06  3.292919e+04
2           0.0   982.401460  ...  2.039757e+05  3.208843e+04
3           0.0   973.794216  ... -2.527055e+05  3.228511e+04
4           0.0   965.262383  ... -7.053975e+05  3.210189e+04
..          ...          ...  ...           ...           ...
116         0.0  1346.032341  ...  2.851405e+04  2.368209e+04
117         0.0  1343.713636  ... -2.927039e+05  2.370171e+04
118         0.0  1341.398924  ...  4.096877e+05  2.347573e+04
119         0.0  1339.088201  ...  4.207922e+05  2.381819e+04
120         0.0     0.000000  ... -3.263268e+07  0.000000e+00

[121 rows x 9 columns]

result_pv() outputs the present values of the cashflows:

>>> result_pv()
      Premiums          Death  ...  Commissions  Net Cashflow
PV  50000000.0  135032.740399  ...    2500000.0  4.957050e+06

result_cf()	Result table of cashflows
result_pv()	Result table of present value of cashflows
result_pols()	Result table of policy decrement

previous

The savings Library

next

proj_len