Black-Scholes-Merton on dividend paying stock

As the 2. Extended Stochastic Example shows, time values of options and guarantees on a GMAB policy can be calculated using the Black-Scholes-Merton formula on a dividend paying stock, when maintenance fees are deducted from account value at a constant rate, by regarding the fees as dividends.

The Black-Scholes-Merton pricing formula for European put options on a dividend paying stock can be expressed as below, where \(X\), \(S_{0}\), \(q\) correspond to the sum assured, the initial account value and the maintenence fee rate(1%) in this example.

\[ \begin{align}\begin{aligned}p=Xe^{-rT}N\left(-d_{2}\right)-S_{0}e^{-qT}N\left(-d_{1}\right)\\d_{1}=d_{1}=\frac{\ln\left(\frac{S_{0}}{X}\right)+\left(r-q+\frac{\sigma^{2}}{2}\right)T}{\sigma\sqrt{T}}\\d_{2}=d_{1}-\sigma\sqrt{T}\end{aligned}\end{align} \]

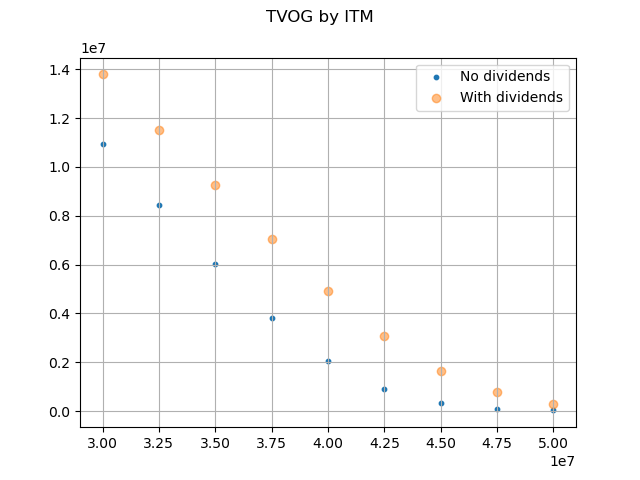
The graph below compares the option values with the maintenance fee deduction against the corresponding values without fee deduction for various in-the-moneyness.

Reference: Options, Futures, and Other Derivatives by John C.Hull

See also

• 1. Simple Stochastic Example notebook in the savings library

• 2. Extended Stochastic Example notebook in the savings library

import modelx as mx
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm, lognorm
import numpy as np

ex1 = mx.read_model("CashValue_ME_EX1").Projection
ex2 = mx.read_model("CashValue_ME_EX2").Projection

ex1.model_point_table = ex1.model_point_moneyness
ex2.model_point_table = ex2.model_point_moneyness
S0 = ex1.model_point_table['premium_pp'] * ex1.model_point_table['policy_count']

fig, ax = plt.subplots()
ax.scatter(S0, ex1.formula_option_put(120), s= 10, alpha=1, label='No dividends')
ax.scatter(S0, ex2.formula_option_put(120), alpha=0.5, label='With dividends')
ax.legend()
ax.grid(True)
fig.suptitle('TVOG by ITM')

ex1.model.close()
ex2.model.close()

Account value to number of policies Dynamic policy decrement