Note
Click here to download the full example code
Account value distribution#
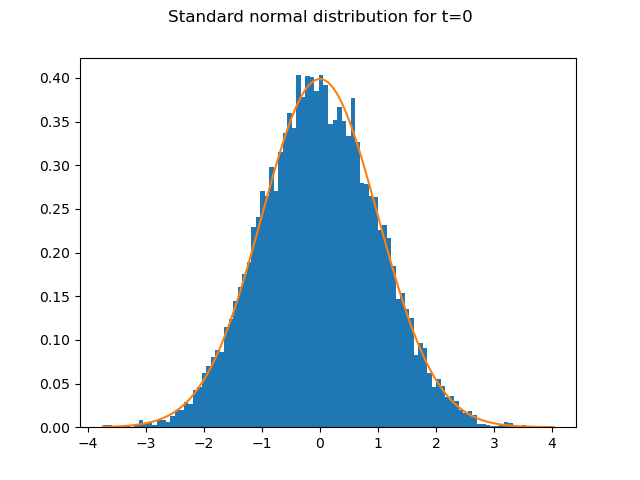
10,000 random numbers drawn from the standard normal distribution
are generated for each time step.
The graph shows how well the 10,000 random numbers for t=0
fit the PDF of the standard normal distribution.
import modelx as mx
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm, lognorm
import numpy as np
model = mx.read_model("CashValue_ME_EX1")
rand_nums = model.Projection.std_norm_rand()
pv_avs = model.Projection.pv_claims_from_av('MATURITY')
num_bins = 100
S0 = 45000000
sigma = 0.03
T = 10
fig, ax = plt.subplots()
n, bins, patches = ax.hist(rand_nums[:, 0], bins=num_bins, density=True)
ax.plot(bins, norm.pdf(bins), '-')
fig.suptitle('Standard normal distribution for t=0')
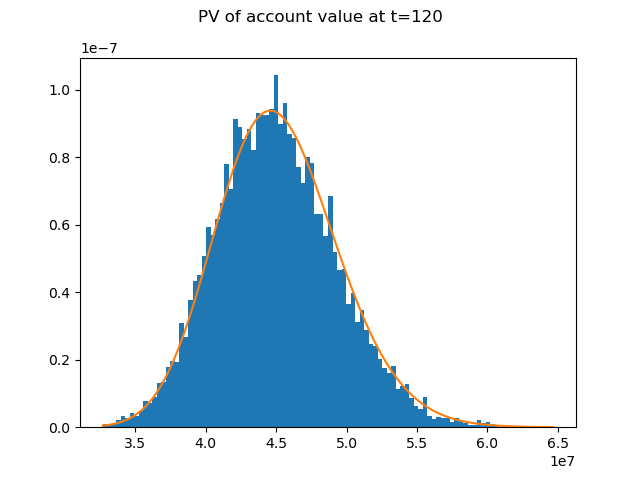
The distibution of the account value at t=120 follows a log normal distribution.
In the expression below, \(S_{T}\) and \(S_{0}\) denote the account value
at t=T=120 and t=0 respectively.
The graph shows how well the distribution of \(e^{-rT}S_{T}\), the present values of the account value at t=0, fits the PDF of a log normal ditribution.
Reference: Options, Futures, and Other Derivatives by John C.Hull
See also
1. Simple Stochastic Example notebook in the
savingslibrary
fig, ax = plt.subplots()
n, bins, patches = ax.hist(pv_avs, bins=num_bins, density=True)
ax.plot(bins, lognorm.pdf(bins, sigma * T**0.5, scale=S0), '-')
fig.suptitle('PV of account value at t=120')
Total running time of the script: ( 0 minutes 2.264 seconds)